See this post for a short primer about the indifference principle and curation mechanics.
The reward curve and the curation curve setup controls how posts get paid and how much curators get. It started with a base set of principles, which ultimately derived what relation the curves must satisfy. One curious property, dubbed the "ultimate indifference principle", is something I'd like to explore more.
This principle states that if you are the last voter, or an indifferent voter, the marginal benefit of voting on a post should be the same regardless of the post. The other interpretation of this is to design a curation system that rewards a minimal base amount, and rewarding a bonus based on discovering a popular post first. The original idea is that later voters should give up a piece of their curation to earlier voters, but instead of explicitly computing this sort of referral on every vote, you model with secondary claims on a properly designed curve.
Motivations for keeping the "Ultimate Indifference Principle"
Let the curation curve be C(r), and the rewards curve be R(r), where the input r is the rshares on a given post.
We showed in the reference post that the marginal curation rewards for voting on a post is given by
C'(r)/C(r) * R(r) * (rewards/claims)
If
C'/C*Ris an increasing function ofr, it encourages lazy curation. Why? Because you can get an amount vastly disproportionate to your stake simply by voting on the most popular post that you see. And a system where a trivial plan like that can reward you so much is just a disaster (even easier than linear farming). And just imagine what you get if you are not last either. Curator's Runaway Paradise.If
C'/C*Ris a decreasing function ofr, the opposite happens. It's less bad, because it is a check on popular posts continuing to snowball but it also means that even if people like a popular post they would be discouraged from voting on it due to degrading returns. An indifferent curator is motivated to vote on posts that don't have value at all vs ones that already have value.
But actually, there's a simplicity to giving any curator a small base amount to motivate a curation, and grant bonuses based on how well their choice did. And that's really what this property captures.
If a curation system that makes use of the two curves is considering deviating from known previous pairs of curves, I would highly recommend checking that it satisfies this principle.
PAL?
The current property of PAL is r^1.05 rewards curve and r^0.5 curation. Plugging in the formulas show that the marginal reward for a post at r rshares is
C'/C*R*(fund/claims) = 0.5 r^0.05 * (fund/claims), an increasing function of r, as in the first category above.
Problem??
First, a comparison of relative choices. At the top of trending you have posts with on the order of 100k rshares. Compared to a post with say 1000 rshares, it already gives a bonus multiplier of 1.25x (25% more impact for a post with 100x the rshares).
This is if you are the last voter. We don't know what will happen eventually, but there should not be such a boost to vote on already popular posts. It ought to be neutral.
However, the numbers I picked there show that the bonus is rather mild. Also note that if we plug in recent claims and reward numbers, the benefit per rshare for a post at 100k rshares is
0.5 * (100000)^.05 * (2349 / 58458681) = 0.00003572761 PAL
which as you can see is pretty minor. So you really need to be one of the first voters to get any real curation benefits, as even the bonus for voting already popular posts is not great.
It could eventually become a problem in theory with token inflation and if people do end up stacking votes very high, but the range where that becomes a problem is not in reach for the time being.
I take this to mean that with the current settings things are okay, in that there does not seem to be a vector for abuse. But in the ideal, as mentioned above, there should not be extra or less incentive to vote on a post purely on the basis that it has more votes.
I have a proposed curve that addresses this, and it also makes things more equitable.
The curve that actually satisfies the indifference property, as computed in the reference post, is of the form exp(-kr^-.05) for some k. And where k can be tuned so that
.05*k*(reward pool) / (recent claims) = target minimum per rshare reward
However, there's another condition that needs attention. The derivative of the curation curve should be always positive (which is true) and decreasing in the relevant range (as more votes are added the marginal curation benefit should be decreasing). This condition is found by taking the second derivative:
exp(-kr^-.05)*((.05 *k* r^-1.05)^2 - 1.05 * 0.5 * k * r^-2.05)) < 0
The transition is at:
(k / 21)^20 = r
where it is negative after this point and positive before.
Roughly, k needs to be less than or equal to 21.
So the best we can make the minimum reward is to set k to be 21, in which case the minimum curation reward is set to .0004 per rshare, regardless of what or when you vote.
Here's what the graph looks like comparing the two curves...
https://www.desmos.com/calculator/aqf3bjyhfh
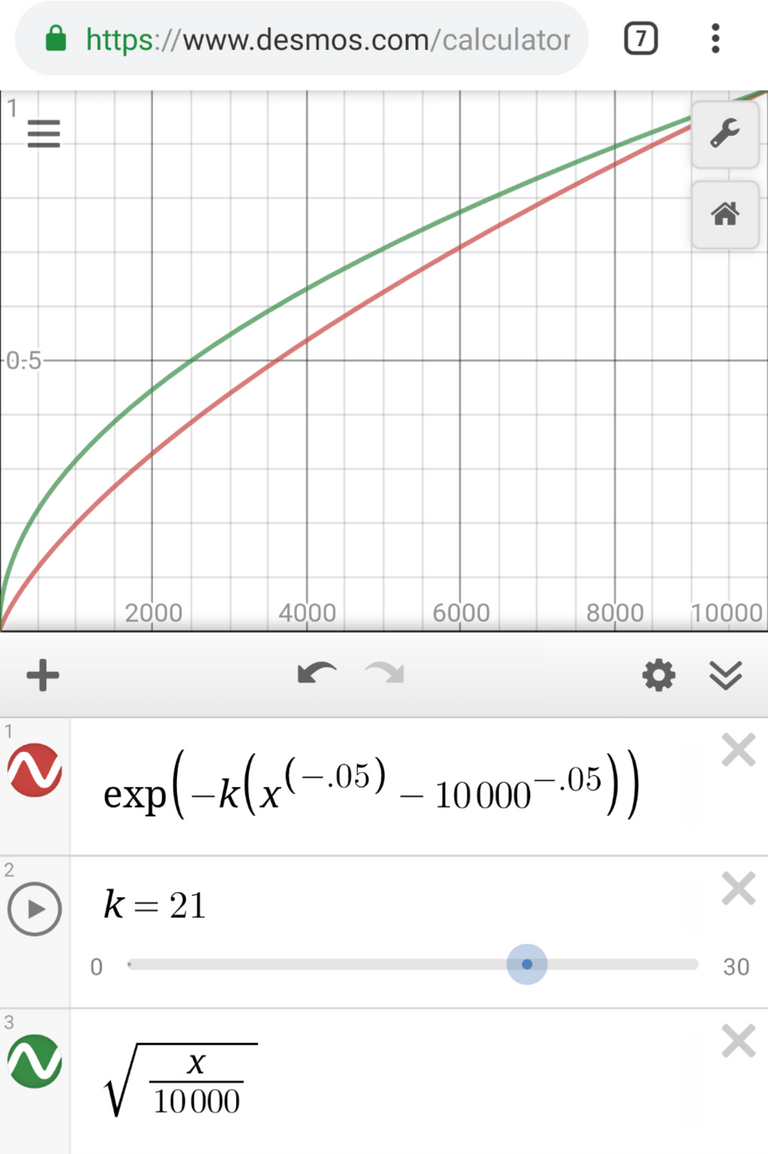
This compares the effect of the curation curve for a post that has 10000 rshares. You can see that the two formulas yield similar curves, and you can also play with the scaling of k to see how it affects earlier voters. The larger values of k are more equitable but too high and the curve becomes broken (increasing rewards to late votes).
This post mainly serves as a suggestion to change the curation curve to one that matches base principles, and an appeal to anyone that's playing with author and curation exponents to consult a mathematician at the very least to analyze impact.
Posted using Partiko Android
