Last week, I released a new scientific article on a topic that I work on since 2013. Six years of work summarised in 70 pages are now (freely) available from here.
This piece of work, addressing computer simulations, required a lot of efforts and I am happy to explain here why it is relevant and what this will change for the high-energy physics community.

[image credits: Free-Photos (Pixabay) ]
Particle physicists dealing with collider studies, such as at those at the CERN Large Hadron Collider (the LHC) or any future project like the 100km-long FCC collider project, need to simulate billions of collisions on computers to understand what is going on.
This holds both for the background of the Standard Model and for any potential signal of a new phenomenon.
Tremendous efforts have been made for what concerns the former. While the Standard Model of particle physics is a well established theory, we still want to test it at its deepest level. To this aim, we need extremely accurate predictions to verify that there is not any deviation when the theory is compared with the experiment.
Developments of the last couple of decades have allowed to reach this goal. Any process of the Standard Model (i.e. the production of several known particles at colliders like the LHC) can today be simulated with an impressive precision.
On different grounds, this also means that the background to any potentially observable new phenomenon is well controlled. In contrast, simulations of any signal of a new phenomenon are usually much cruder.
This is the problem that is tackled in my research article: simulations describing any process in any model (extending the Standard Model) can now be systematically and automatically achieved at a good level of precision.
Quantum field theory in a nutshell
The calculation of any quantity observable at colliders typically requires the numerical evaluation of complex integrals. Such integrals represent the sum of all the ways to produce a given set of particles. They can for instance be produced with one of them recoiling against all the others or with a pair of them being back-to-back. Every single available option is included in the integral.

[image credits: Pcharito (CC BY-SA 3.0) ]
One element of the calculation indicates how the particle physics model allows for the production of the final-state particles of interests.
This element is hence highly model-dependent: if one changes the model, one changes the manner to produce a specific final-state system.
Moreover, there also is some process-dependence: if one considers other particles to be produced, it is simply a different calculation.
This is where an automated and systematic approach wins: it works regardless the process and regardless the model. The only thing the physicist has to do is to plug in the model of his/her dream, and the process he/she is interested in.
Such an option actually exists for many years, as can be read in this article that I wrote already 10 years ago. The difference with respect to the article of last week lies in a single keyword: precision (in contrast to crude predictions as in my old article of 2009).
Precision predictions for new phenomena
Let’s go back for a minute to this model-dependent and process-dependent piece of the calculation. Its evaluation relies on perturbation theory, so that its analytical form can be organised as an infinite sum. Each term of the sum depends on a given power in a small parameter called as: the first component is proportional to as, the second to as2, and so on.

[image credits: Wolfgang Beyer (CC BY-SA 3.0) ]
Solely computing the first component of the series allows one to get the order of magnitude of the full result, with a huge error resulting from the truncation of the series to this leading-order piece.
The second component contributes as a small correction, but at the same time allows for a significant reduction of the uncertainties. This next-to-leading-order prediction is therefore more precise.
And so on… Higher orders lead smaller and smaller contributions together with a more and more precise outcome.
The problem is that whilst the leading-order piece is something fairly easy to calculate, the next-to-leading-order one starts to be tough and the next ones are even harder. The reason lies in infinities appearing all over the place and canceling each other. However, at the numerical level, dealing with infinities is an issue so that appropriate methods need to be designed.
My new research article provided the last missing ingredients to deal with next-to-leading order calculations of any process in any theory can now be achieved systematically and automatically.
An example to finish and conclude
I present below the distribution of a physical quantity relevant for the searches of hypothetical particles called quarks and gluinos at the LHC (this is the x-axis). The y-axis shows the rate of new phenomena for given values of the physical quantity.
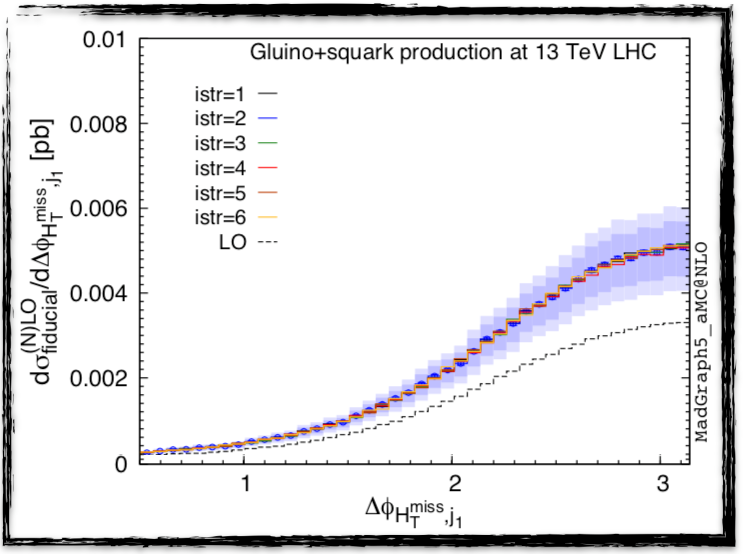
[image credits: arXiv ]
The black dashed curve consists in the leading-order prediction (we truncate the series to its first component) whilst the solid red line in the middle of the blue band consists in the next-to-leading order result (we truncate the series to the sum of its first and second components). The impact of the next-to-leading-order correction is clearly visible when comparing the dashed black line with the solid red line: there is a large shift in the predictions.
The uncertainties attached with the leading order curve are not shown as very large. The next-to-leading order ones represented by the blue bands. The improvement is described in the research article itself: we move from a 30%-45% level of precision (at leading order) to a 20% level of precision (at the next-to-leading order).
To summarise, new phenomena searched for at colliders can now be precisely, systematically and automatically computed, which is crucial for our understanding of any potential excess that could be found in data in the up-coming years. Moreover, all codes that have been developed are public, open source, and are efficient enough to run on standard laptops.
SteemSTEM
SteemSTEM aims to make Steem a better place for Science, Technology, Engineering and Mathematics (STEM) and to build a science communication platform on Steem.
Make sure to follow SteemSTEM on steemstem.io, Steemit, Facebook, Twitter and Instagram to always be up-to-date on our latest news and ideas. Please also consider to support the project by supporting our witness (@stem.witness) or by delegating to @steemstem for a ROI of 65% of our curation rewards (quick delegation links: 50SP | 100SP | 500SP | 1000SP | 5000SP | 10000SP).
